Radicali
13.10.2015 17:43

În matematică, radicalul unui număr reprezintă un alt număr, care ridicat la o putere (denumită ordinul radicalului) este egal cu numărul dat. Dacă ordinul unui radical nu este precizat, atunci este vorba implicit de radicalul de ordinul 2, denumit șirădăcină pătrată; fiecare număr real pozitiv  are două rădăcini pătrate:
are două rădăcini pătrate:  , iar fiecare număr real negativ are două rădăcini pătrate complexe conjugate:
, iar fiecare număr real negativ are două rădăcini pătrate complexe conjugate:  .
.

Definiții
- Fie
 și
și 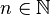 un număr natural nenul. Se numește radical de ordinul
un număr natural nenul. Se numește radical de ordinul  acel număr pozitiv
acel număr pozitiv  pentru care
pentru care 
- Fie
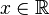 și
și 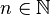 un număr natural nenul. Se numește radical de oridinul
un număr natural nenul. Se numește radical de oridinul 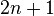 acel număr real
acel număr real  pentru care
pentru care 
Notații:
![\sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) - radicalul de ordin n al lui x.
- radicalul de ordin n al lui x. - radicalul de ordin 2
- radicalul de ordin 2
Exemple
Rădăcinile pătrate ale primelor 20 de numere naturale[modificare | modificare sursă]
-


1 

1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462 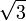

1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909 

2 

2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638 

2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457 

2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230 

2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924 

3 

3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639 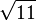

3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609 

3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818 

3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293 

3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307 

3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937 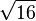

4 

4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338 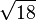

4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386 

4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203 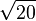

4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
Operații cu radicali
- Radicalul unui produs de numere raționale pozitive este egal cu produsul radicalilor numerelor raționale respective:

- Radicalul inversului unui număr rațional pozitiv este egal cu inversul radicalului numărului:

- Radicalul câtului a două numere raționale pozitive este egal cu câtul radicalilor celor două numere raționale:

- Adunarea numerelor
 și
și  , se face dupǎ regula:
, se face dupǎ regula: 
- Scǎderea numerelor
 și
și  , se face dupǎ regula:
, se face dupǎ regula: 
- Înmulțirea numerelor
 și
și , se face după regula:
, se face după regula: 
